MMO Script is a simplified new way to build and scale your game with a seamless deployment pipeline for launching and multiplexing servers.


MMO Script is a simplified new way to build and scale your game with a seamless deployment pipeline for launching and multiplexing servers.

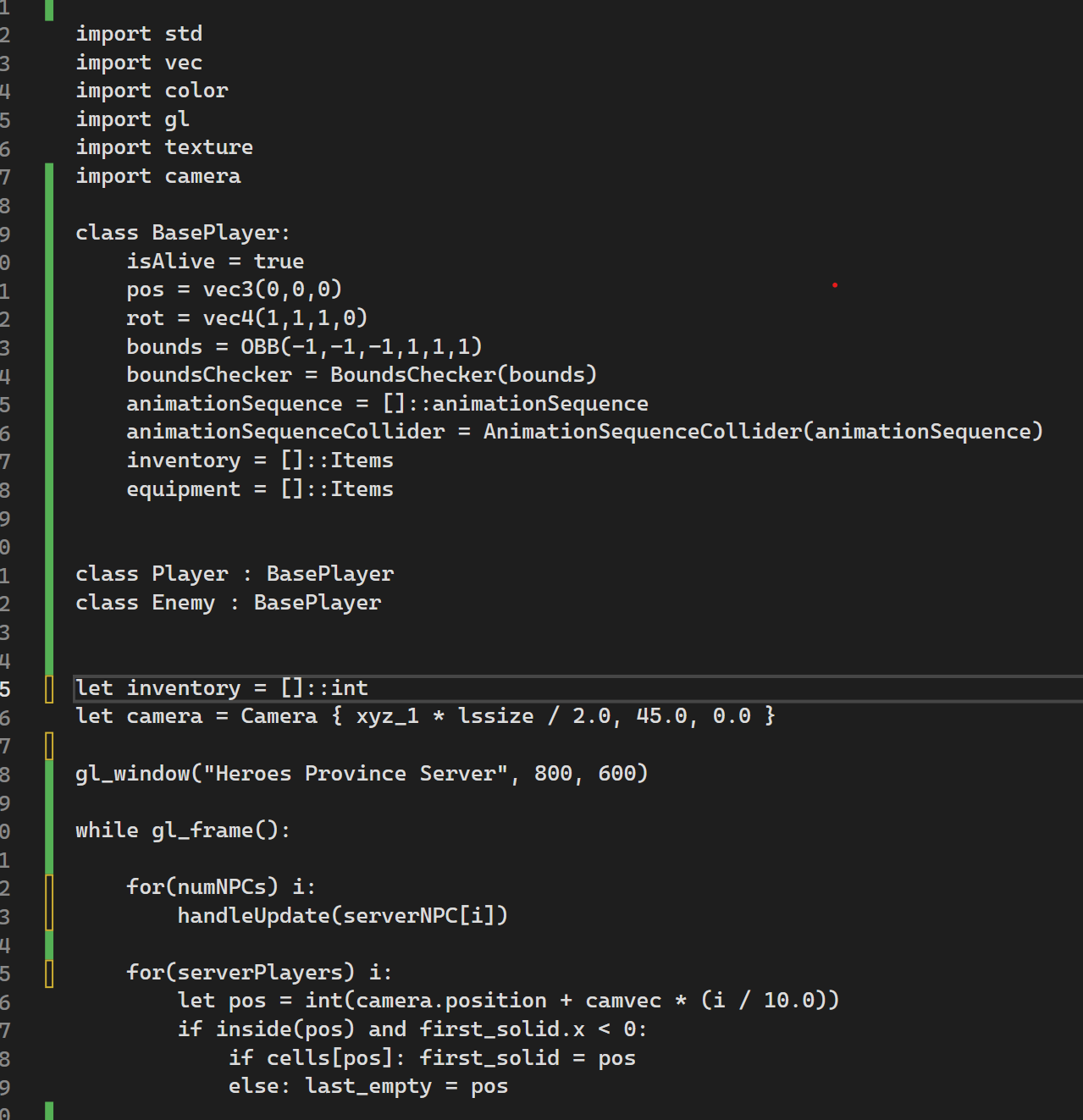
In this blog we talk about MMO Script and how it can be used to simplify the aspects of multiplexing servers that share game logic to support a stable, redundant, and seamless runtime across the network.

In this NEW Blog we explore the design of the Heroes Province client-server combat system and server authoritative combat in an asynchronous real-time multiplayer game.


(Work in Progress)
See this new Chipper Chickadee blog exploring the Heroes Province Server Architecture.
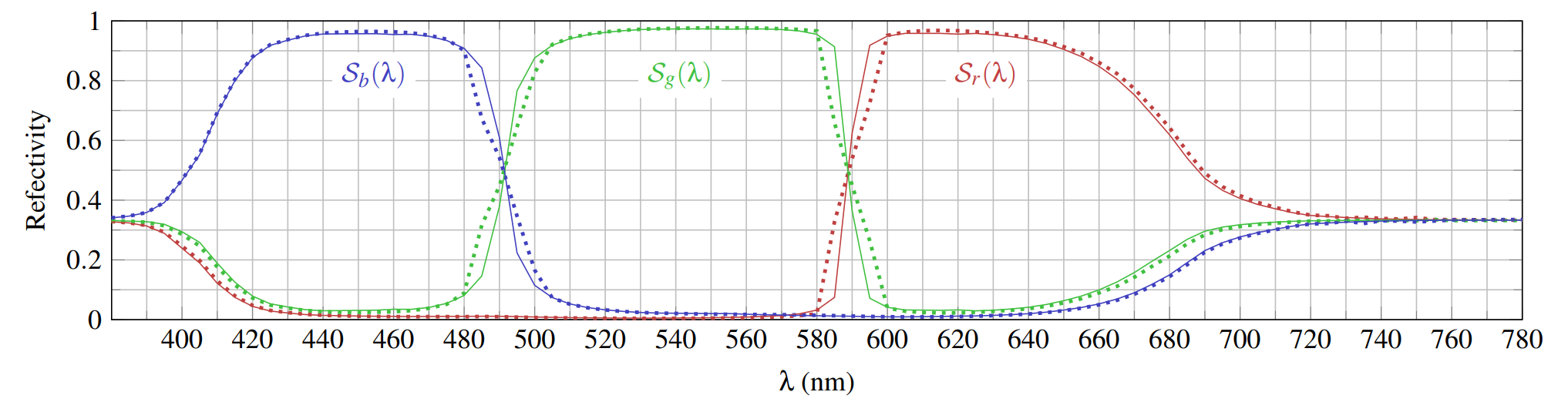
Courtesy of https://graphics.geometrian.com/research/spectral-primaries.html
Spectral Primary Decomposition is a technique used in computer graphics and rendering to efficiently generate a reflectance spectrum from sRGB input data1, 2. It involves decomposing the sRGB reflectance spectrum into a linear combination of three pre-computed spectral primaries, each corresponding to one of the three primary color components (red, green, and blue) 3. The Spectral Primary Decomposition technique allows for efficient computation of reflectance spectra by using a small set of pre-computed spectral primaries. This reduces the computational complexity compared to directly representing the reflectance spectrum with a large number of samples, t can be used for computing reflectance spectra from sRGB input data.
Here is a GLSL example of decomposing sRGB texture values into spectral primaries.
// Define the spectral primaries
uniform sampler2D redPrimary;
uniform sampler2D greenPrimary;
uniform sampler2D bluePrimary;
// Convert sRGB to linear RGB
vec3 linearRGB = pow(texture(sRGBTexture, texCoord).rgb, vec3(2.2));
// Compute the coefficients for the linear combination of the spectral primaries
mat3 spectralMatrix = mat3(
texture(redPrimary, texCoord).rgb,
texture(greenPrimary, texCoord).rgb,
texture(bluePrimary, texCoord).rgb
);
vec3 spectralCoefficients = inverse(spectralMatrix) * linearRGB;
// Multiply the coefficients with the spectral primaries to obtain the final reflectance spectrum
vec3 reflectanceSpectrum = spectralCoefficients.r * texture(redPrimary, texCoord).rgb
+ spectralCoefficients.g * texture(greenPrimary, texCoord).rgb
+ spectralCoefficients.b * texture(bluePrimary, texCoord).rgb;
CIE stands for the International Commission on Illumination, which is responsible for defining the CIE color spaces and standard illuminants used in colorimetry and spectral rendering.
The CIE color system characterizes colors by a luminance parameter Y and two color coordinates x and y, which specify the point on the chromaticity diagram.
The image below is the CIE chromaticity diagram for the sRGB color space, where the corners of the triangle represent the primary R, G, B colors. Colors outside of the triangle cannot be represented on an sRGB monitor.
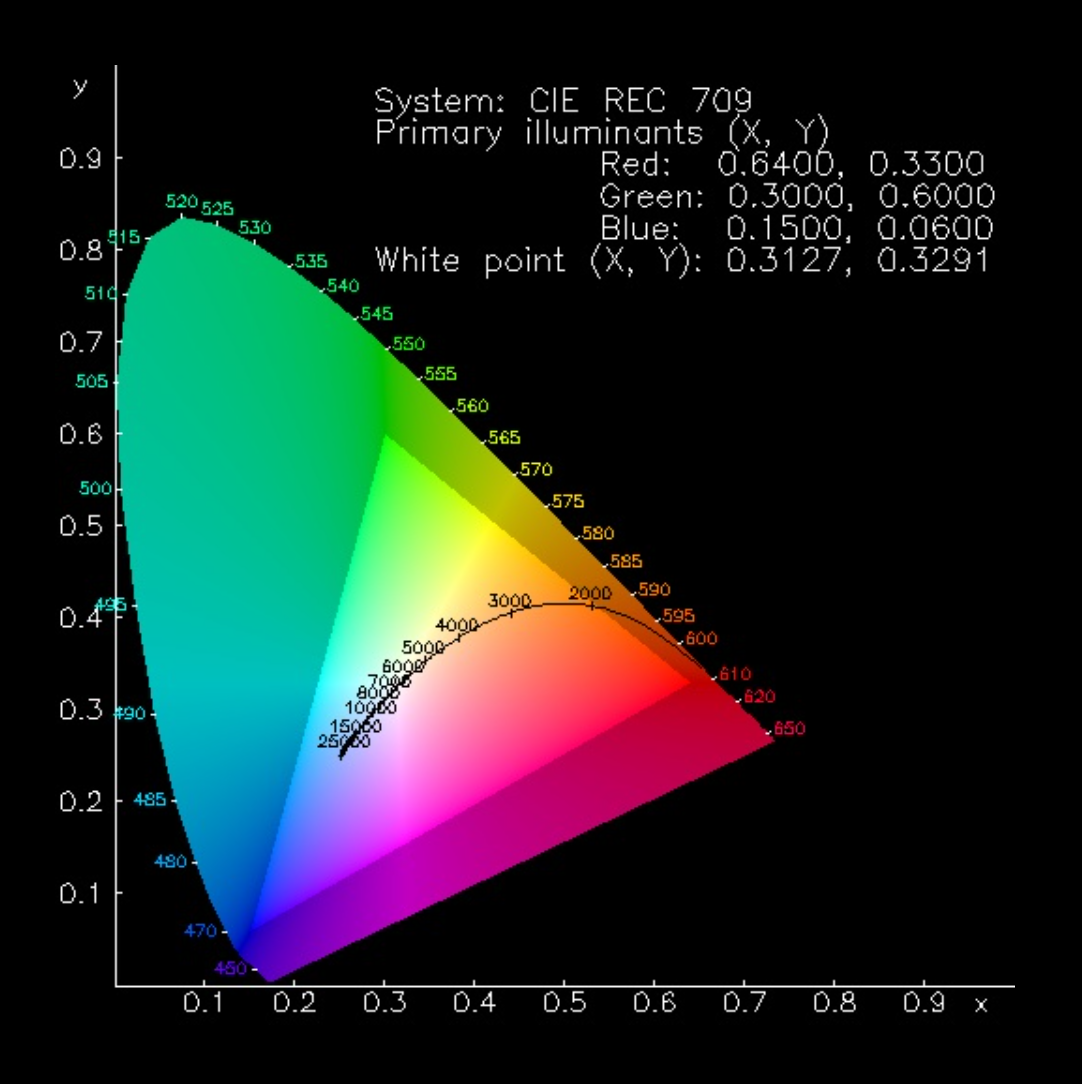
Courtesy of Rendering Spectra
To convert from CIE XYZ coordinates to sRGB in a GLSL shader, you can use the following code:
vec3 convertXYZtoRGB(vec3 XYZ) {
mat3 XYZtoRGB = mat3(3.2406, -1.5372, -0.4986,
-0.9689, 1.8758, 0.0415,
0.0557, -0.2040, 1.0570);
vec3 RGB = XYZtoRGB * XYZ;
return RGB;
}
void main() {
// Define the CIE XYZ values
vec3 XYZ = vec3(0.25, 0.40, 0.10);
// Convert from CIE XYZ to sRGB
vec3 sRGB = convertXYZtoRGB(XYZ);
// Output the sRGB color
gl_FragColor = vec4(sRGB, 1.0);
}Combining relative and metric depth refers to a technique that integrates both relative depth information and metric depth information to improve depth estimation.

Relative Depth: Relative depth refers to the ordering of objects in a scene based on their distances from the camera. It provides information about the depth ordering but not the actual metric distances. Relative depth can be estimated using techniques such as monocular depth estimation or stereo vision.
Metric Depth: Metric depth refers to the actual distance of objects from the camera, typically measured in real-world units like meters or feet. It provides precise depth information but may require calibration and additional sensors.
By incorporating relative depth information, the algorithm can capture the depth ordering of objects in the scene. At the same time, by incorporating metric depth information, the algorithm can obtain accurate distance measurements.
One approach to combining relative and metric depth is through the use of deep learning techniques. For example, the ZoeDepth algorithm combines relative and metric depth estimation by training a neural network to predict both relative depth and metric depth from a single image. This allows the algorithm to capture the depth ordering of objects while also providing accurate depth measurements.

Making a fire in Heroes Province will help keep you safe from the nighttime creatures.

But do not stray too far from camp or you may be caught off guard!


Rendering reflections in Augmented Reality can be very difficult. Reflection surfaces must work with plane detection to compute a reflection normal. The color and texture of the reflection can be fine tuned to match the surface. In addition, the reflection must be clipped against the background. To do this we explore the paper “Active Contours without Edges” in the Chipper Chickadee development blog HERE.
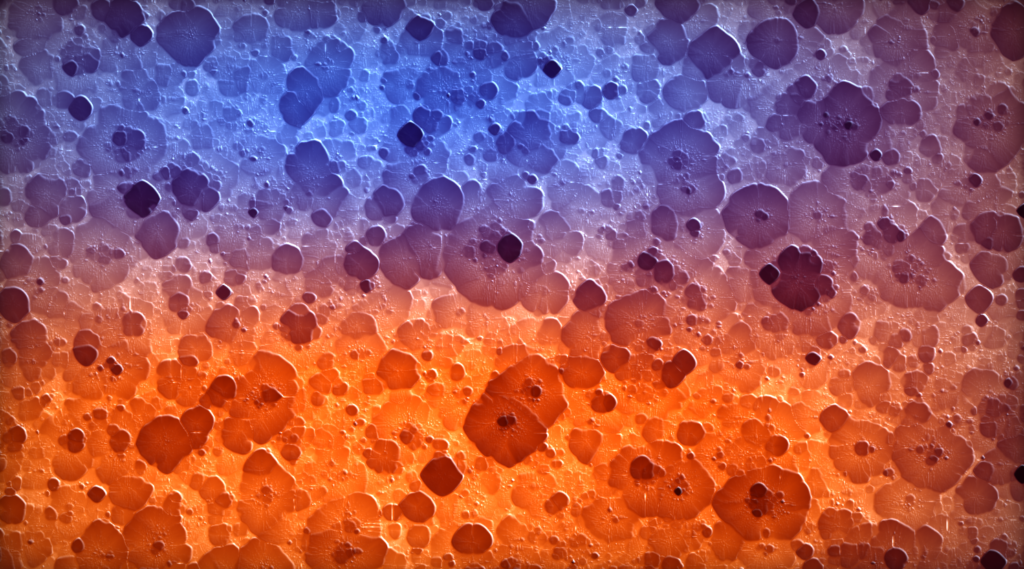
I was looking for procedural ways to make organic looking textures and started studying Reaction-diffusion Systems. Reaction-diffusion systems can generate a wide range of interesting patterns and textures. This course provides examples of reaction-diffusion phenomena that you can implement using shaders.

Heroes Province is getting Unreal 5 support. Here is a sneak peak.

Making a camp is the first step for survival

If you don’t fence in your garden the deer will eat all your vegetables.



This demonstrates real-time server based subsurface scattering in augmented reality using lighting generated from capture.
We have a new website at http://delta3d.io
All prior releases can be found at the source forge project page-
http://sourceforge.net/projects/delta3d


This is a sneak preview of a game we are currently working on. We will be posting the first playable version this weekend, stay tuned!
Chipper Chickadee Studios is a game development and contracting company based in Virginia Beach, Virginia. We have been supporting local groups with software development, art creation, and level design services for over 10 years and have come together to create Heroes Province, a unique puzzle rpg adventure where you must build a province and protect it.

Hooray for Chipper Chickadee Studios.