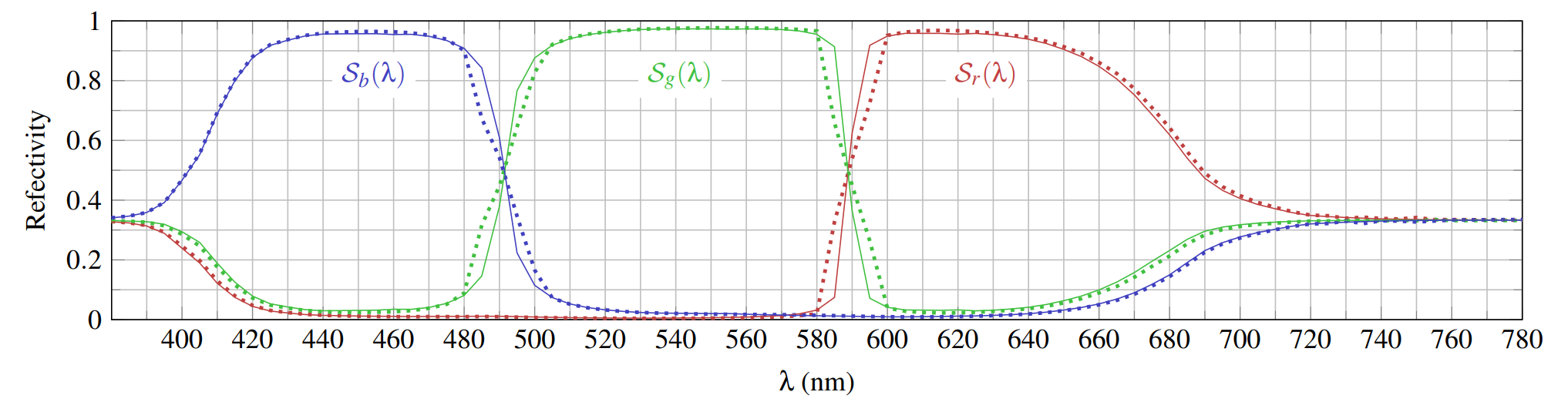
Courtesy of https://graphics.geometrian.com/research/spectral-primaries.html

Spectral Primary Decomposition is a technique used in computer graphics and rendering to efficiently generate a reflectance spectrum from sRGB input data1, 2. It involves decomposing the sRGB reflectance spectrum into a linear combination of three pre-computed spectral primaries, each corresponding to one of the three primary color components (red, green, and blue) 3. The Spectral Primary Decomposition technique allows for efficient computation of reflectance spectra by using a small set of pre-computed spectral primaries. This reduces the computational complexity compared to directly representing the reflectance spectrum with a large number of samples, t can be used for computing reflectance spectra from sRGB input data.

Here is a GLSL example of decomposing sRGB texture values into spectral primaries.

// Define the spectral primaries
uniform sampler2D redPrimary;
uniform sampler2D greenPrimary;
uniform sampler2D bluePrimary;

// Convert sRGB to linear RGB
vec3 linearRGB = pow(texture(sRGBTexture, texCoord).rgb, vec3(2.2));

// Compute the coefficients for the linear combination of the spectral primaries
mat3 spectralMatrix = mat3(
    texture(redPrimary, texCoord).rgb,
    texture(greenPrimary, texCoord).rgb,
    texture(bluePrimary, texCoord).rgb
);
vec3 spectralCoefficients = inverse(spectralMatrix) * linearRGB;

// Multiply the coefficients with the spectral primaries to obtain the final reflectance spectrum
vec3 reflectanceSpectrum = spectralCoefficients.r * texture(redPrimary, texCoord).rgb
                         + spectralCoefficients.g * texture(greenPrimary, texCoord).rgb
                         + spectralCoefficients.b * texture(bluePrimary, texCoord).rgb;